直方图

什么是直方图？

直方图是一种图表，它将数值变量的值分布以一系列条形表示。每个条形通常覆盖一个数值范围，称为箱或类别；条形的高度表示对应箱内数据点的频率。

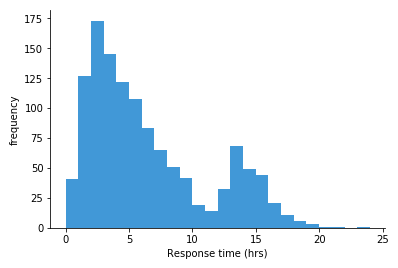
上面的直方图显示了虚构支持系统中工单响应时间的频率分布。每个条形覆盖一个小时的时间，高度表示每个时间范围内的工单数量。我们可以看到，响应频率最高的范围是2-3小时，右侧的尾部比左侧更长。还有一个较小的山峰，其峰值（众数）位于13-14小时范围。如果我们只看均值和标准差等数值统计，可能会忽略这两个峰对整体统计数据的贡献。

何时使用直方图

直方图适用于展示数据集变量的总体分布特征。你可以大致看到分布的峰值位置、分布是否偏斜或对称，以及是否存在异常值。

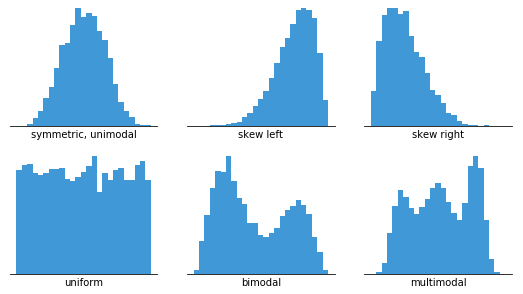
要使用直方图，我们只需要一个取连续数值的变量。这意味着数值之间的差异是始终一致的，无论其绝对值如何。例如，即使考试成绩可能只取0到100之间的整数值，无论在刻度上的哪个位置，相同大小的间隔都有相同的意义：60和65之间的差异与90到95之间的差异都是同样5分的大小。

关于数据点统计的箱数及其边界的信息并非数据本身固有。相反，设置箱子是一个我们在构建直方图时必须做出的独立决策。我们指定箱子的方式将极大地影响直方图的可解释性，如下文所示。

当数值位于箱边界上时，它将始终被分配到其右侧或左侧的箱（如果位于端点，则分配到端箱）。选择哪一侧取决于可视化工具；某些工具提供选项来覆盖其默认偏好。在本文中，将假设位于箱边界上的数值将被分配到右侧的箱。

数据结构示例

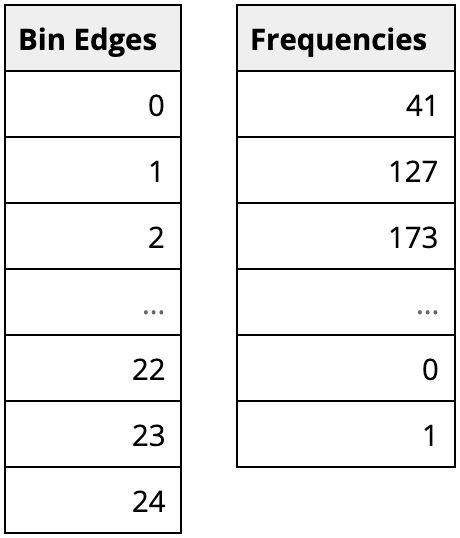
可视化工具处理数据以将其可视化为直方图的一种方式是使用类似于上述的汇总形式。这里，第一列表示箱边界，第二列表示每个箱中的观测次数。或者，某些工具可以直接处理原始的未聚合数据列，然后在创建直方图时将指定的分箱参数应用于数据。

使用直方图的最佳实践

使用零值基线

直方图的一个重要方面是它们必须以零值基线绘制。由于每个箱中数据的频率由每个条形的高度隐含表示，改变基线或在刻度中引入间隙会扭曲对数据分布的感知。

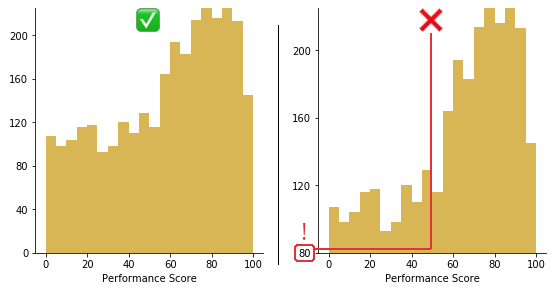
从垂直轴上剪切80个点，使得性能分数的分布看起来比实际情况好得多。

选择合适的箱子数量

虽然能够生成直方图的工具通常内置了一些默认算法来选择分组边界，但你很可能需要调整分组参数，以选择能代表你数据的方案。维基百科有一个关于选择合适分组数量和大小的经验法则的详细章节，但最终，结合领域知识和尝试多种选项，才能知道哪种方案最适合你的需求。

分组大小与分组数量成反比关系。分组越大，覆盖整个数据范围的分组数量就越少。分组越小，需要的分组数量就越多。值得花些时间测试不同的分组大小，看看每种情况下的数据分布情况，然后选择最能代表数据的图表。如果分组过多，数据分布会显得粗糙，难以从噪声中分辨出信号。另一方面，如果分组过少，直方图会缺乏分辨数据中任何有用模式所需的细节。

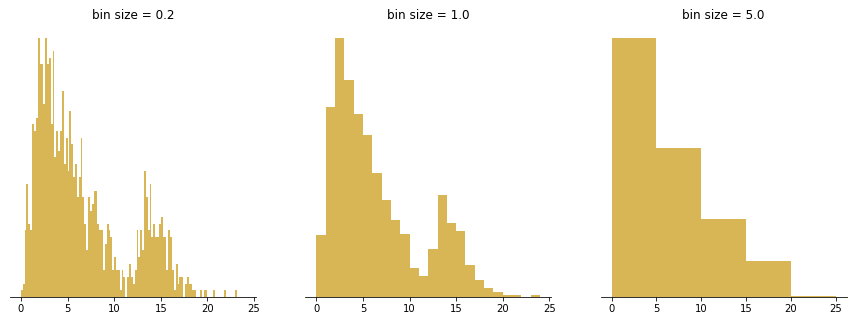
左边的面板的箱子太小，意味着有很多虚假的峰值和谷值。右边的面板的箱子太大，隐藏了第二个峰值的任何迹象。

选择可解释的直方图边界

刻度标记和标签通常应落在箱子的边界上，以便最好地告知每个条形的界限在哪里。标签不需要为每个条形设置，但每隔几个条形设置一个标签有助于读者跟踪数值。此外，如果标签是只有少数几个有效数字  的值，使它们易于阅读，那就很有帮助。

这表明大小为1、2、2.5、4或5的箱子（这些箱子可以均等地划分5、10和20）或它们的十进制幂是作为经验法则的良好箱子大小开始。这也意味着大小为3、7或9的箱子可能更难阅读，除非上下文适合使用它们，否则不应使用。

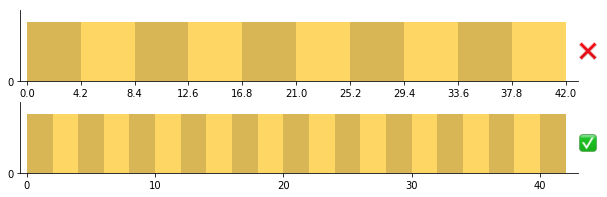
顶部：从最小值到最大值随意将数据分成十个箱子，可能会导致非常奇怪的箱子划分。底部：当箱子大小容易理解时，需要的刻度标记就较少。

一点小提醒：确保你考虑了感兴趣变量的取值类型。在分数字段大小如2.5的情况下，如果变量只取整数值，这可能会成为问题。一个从0到2.5的区间有机会收集三个不同的值（0、1、2），但接下来的从2.5到5的区间只能收集两个不同的值（3、4——5会落入下一个区间）。这意味着你的直方图可能会因为每个区间可能收集的值的数量而显得不自然地“崎岖不平”。

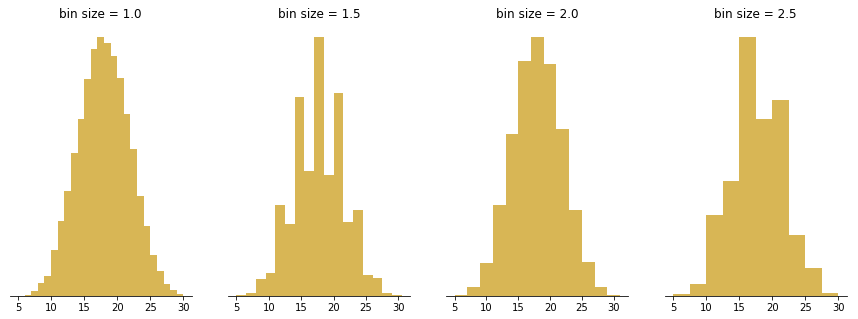
上图展示了将五个骰子的结果相加，重复20000次时的结果分布情况。当选择捕获不同数量整数结果的分组大小不同时，预期的钟形曲线看起来会参差不齐或偏斜。

常见误用

测量变量不是连续数值

如开篇所述，直方图旨在描绘连续数值变量的频率分布。当我们的目标变量不具备这一特性时，我们需要使用其他类型的图表：条形图。取分类值的变量，如用户类型（例如访客、用户）或位置，显然不是数值型，因此应使用条形图。然而，某些变量类型可能更难分类：取离散数值的变量和取时间值的变量。

取离散数值的变量（例如整数1、2、3等）可以用条形图或直方图绘制，具体取决于上下文。当有大量不同的值需要绘制时，更可能使用直方图。当数值范围较大时，离散值这一事实往往不重要，连续分组会是个好主意。

需要注意的一个主要问题是数字要能代表实际数值。如果数字实际上是分类变量或松散排序变量的代码，那么就应该使用条形图。例如，如果你有一个从1到5的量表上的调查回复，编码从“强烈反对”到“强烈同意”的值，那么频率分布应该用条形图来可视化。原因是个体值之间的差异可能并不一致：我们并不知道1和2之间的有意义差异（“强烈反对”到“反对”）与2和3之间的差异（“反对”到“既不赞同也不反对”）是否相同。

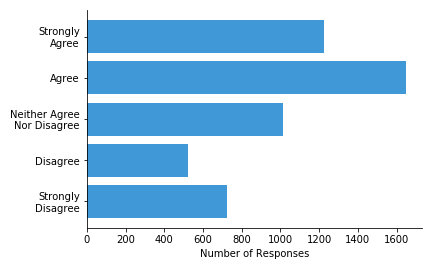
一个更复杂的情况是我们的目标变量是一个基于时间的特征。当值对应于相对时间段（例如 30 秒、20 分钟）时，按时间段对直方图进行分箱是有意义的。然而，当值对应于绝对时间（例如 1 月 10 日 12:15）时，这种区别就会变得模糊。当记录新的数据点时，值通常会进入新创建的箱中，而不是进入现有范围的箱内。此外，某些自然的分组选择，如按月份或季度，会引入略微不等的箱大小。由于这些原因，使用不同的图表类型（如条形图或折线图 ）并不罕见。

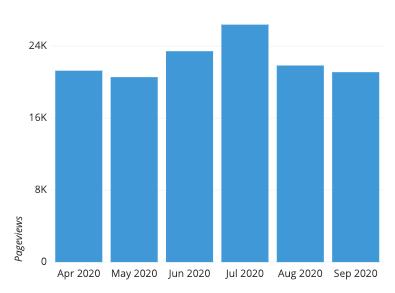
使用不等宽的箱子

虽然到目前为止的所有示例都展示了使用等宽分箱的直方图，但这实际上并不是一个技术要求。当数据稀疏时，比如存在长数据尾，可能会想到使用更大的分箱宽度来覆盖这些空间。然而，创建一个分箱不等宽的直方图并不是严格意义上的错误，但这样做需要对直方图的创建方式做出一些重大改变，并可能造成很多解释上的困难。

直方图的技术要点在于，所有条形的总面积代表整体，而每个条形占据的面积则代表每个区间内包含的整体比例。当区间大小一致时，测量条形面积和高度是等效的。然而，在区间大小不固定的直方图中，高度就无法再与总出现频率相对应。这样做会扭曲对每个区间内有多少点的感知，因为增加区间大小只会让它看起来更大。在下面图形的中间图中，5-6、6-7和7-10区间的条形看起来包含的点数比实际要多。

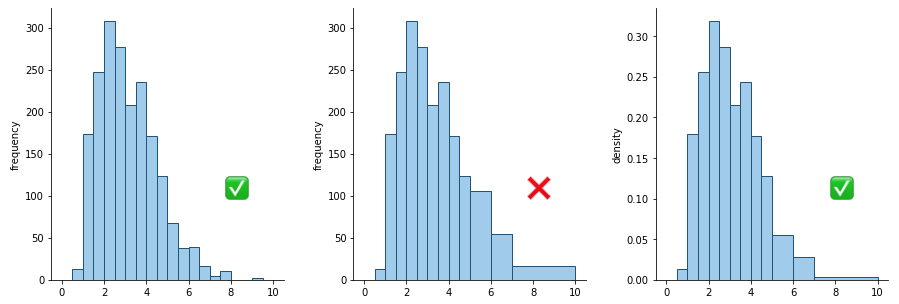
左侧：等宽箱的直方图；中间：不等宽箱但垂直轴单位不当的直方图；右侧：不等宽箱且密度高度的直方图

相反，垂直轴需要编码每个箱子大小的频率密度。例如，在上图右侧的窗格中，从2到2.5的箱子高度约为0.32。乘以箱子宽度0.5，我们可以估计该箱子中约有16%的数据。与中间窗格相比，较宽箱子的高度已被缩小：注意整体形状看起来与原始等宽箱子直方图相似。密度是一个不易理解的概念，向不熟悉这一概念的人展示这样的图表将使其难以解读。

由于所有这些原因，最好的建议是尽量使用完全相等的箱子大小。存在空箱子以及在数据稀疏范围内的一些增加的噪声通常值得 histogram 可解释性的提高。另一方面，如果变量本身具有表明箱子大小不均匀的固有方面，那么与其使用不均匀箱子的 histogram，你可能会更倾向于使用条形图。

常见的直方图选项

绝对频率与相对频率

根据您的可视化目标，您可能需要更改图表垂直轴的单位，使其表示绝对频率或相对频率。绝对频率只是每个箱中出现的自然计数，而相对频率是每个箱中出现的比例。轴单位的选择将取决于您想要强调的数据分布的哪些比较。

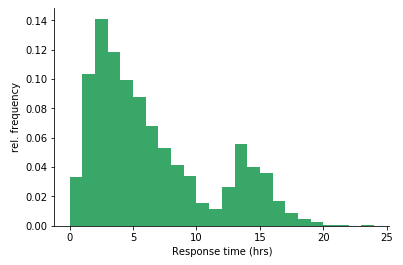
将第一个示例转换为以相对频率表示，更容易将前五个条形图加起来，发现大约一半的票在五小时内得到了回复。

显示未知或缺失数据

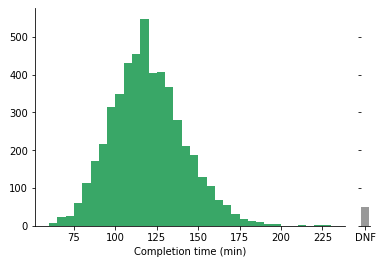
这实际上_并非_  一个特别常见的选项，但在定制图表时值得考虑。如果某行数据在感兴趣变量上缺失值，通常会在每个箱子的统计中跳过。如果显示缺失或未知值的数量很重要，那么你可以将直方图与一个额外的条形图结合，该条形图描绘这些未知值的频率。在绘制这个条形图时，最好将其放在与主直方图平行的轴上，并使用不同的中性颜色，这样收集在该条形图中的点就不会被误认为是数值。

相关图

条形图

如上所述，如果感兴趣变量不是连续的数值型，而是离散型或分类型，那么我们想要使用条形图  。与直方图不同，条形图上的条形之间通常会有一个小间隙：这强调了所绘制变量的离散性。

折线图

如果你已经对数值数据进行了分组，但希望图表的纵轴传达的不仅仅是频率信息，那么你应该考虑使用折线图 。折线图中点的垂直位置可以描绘第二个变量的值或统计摘要。当折线图用于描绘类似于直方图的频率分布时，这被称为频率多边形 。

密度曲线

密度曲线，或称为核密度估计（KDE），是直方图的一种替代方法，它为每个数据点在分布中提供连续的贡献。在直方图中，你可能会将每个数据点想象成将其值倒入一系列下方的圆柱体（即箱子）中。在 KDE 中，每个数据点在其真实值周围添加一小块体积，这些体积在数据点之间堆叠起来，从而生成最终的曲线。体积块的形状是“核”，并且有无限多种选择。由于在选择核及其参数时有大量的选项，密度曲线通常是程序化可视化工具的领域。

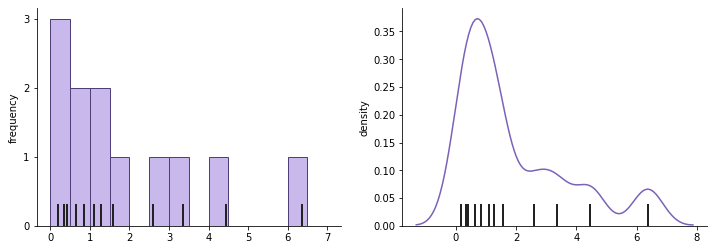
粗黑的虚线表示对直方图（左）和密度曲线（右）有贡献的数据点。注意每个点如何为整体形状贡献一个小钟形曲线。

箱线图和小提琴图

直方图擅长展示单个变量的分布，但如果我们要比较不同组之间的该变量，制作直方图进行比较会有些棘手。对于两组数据，一个可能的解决方案是将两组的直方图并排绘制。这种类型的图在特定领域有一个版本，即人口金字塔 ，它将一个国家或其他地区的男性和女性的年龄分布绘制成并排的垂直直方图。

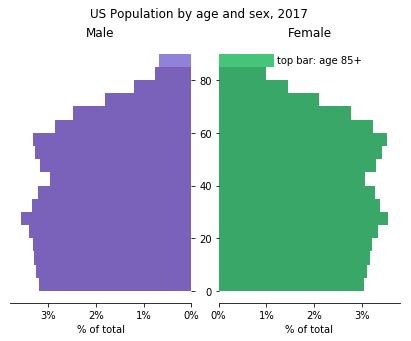
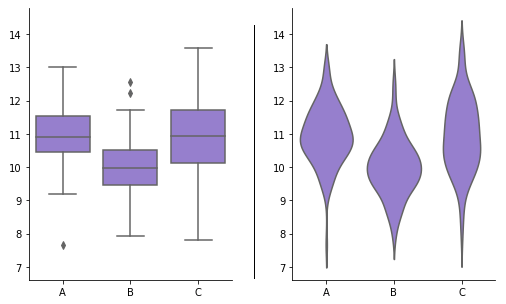
然而，如果我们有三个或更多组，这种首尾相连的解决方案将无法使用。一种解决方案可以是创建分面直方图，在行或列中为每个组绘制一个。另一种替代方案是使用不同的图表类型，例如箱线图 或 小提琴图。这两种图表类型通常用于当我们希望比较数值变量在分类变量不同水平上的分布时。与分面直方图相比，这些图表用更紧凑的分布相对比较来交换绝对频率的准确描绘。

可视化工具

作为一种相当常见的可视化类型，大多数能够生成可视化的工具都会将直方图作为选项之一。如果无法提供直方图，则应使用柱状图作为接近的替代方案。由于需要测试不同的分箱选项以找到最佳方案，创建直方图可能需要比其他基本图表类型稍多的工作。然而，这种努力通常是值得的，因为一个好的直方图可以非常快速且准确地传达数据变量的整体形状和分布情况。

直方图是用于数据可视化的多种图表类型之一。您可以通过阅读我们关于基本图表类型、如何选择数据可视化类型的文章，或浏览图表分类下的全部文章来了解更多信息。