第14章 指标波动归因分析

14.1 指标波动贡献率

什么是贡献率

当核心指标发生了波动，比如销售额从 100 万元上升到 1000 万元时，分析师的工作就来了。这个指标的波动可以从多个维度拆解。

• 渠道维度：天猫渠道、京东渠道、线下渠道等。

• 新老客维度：新客和老客。

• 用户属性维度：年龄、消费力、兴趣偏好、地区。

• 其他底层数据能够支持的维度。

能拆解的维度有很多，但一般来说，数据分析师根据自身经验，会选择一两个主要的维度优先进行拆解和验证。

例如从渠道维度进行拆解，可以进一步细分为 A 渠道、B 渠道、C 渠道这 3 个元素。我们实际关注的是，每一个渠道销售额的变化对于整体销售额波动到底有多大影响。

为了量化每一个元素对总体波动的影响程度，我们引入了“贡献率”的概念。贡献率主要回答“每一个元素的变化对总体波动的贡献是多少”这个问题。通常，各元素贡献率之和等于 $100\mathrm{\%}$ 正好可以完全解释总体波动。

需要强调的是，为了避免概念产生歧义，在本章的销售拆解中，渠道、用户、地区是指不同的维度，而渠道下面的具体渠道值 A、B、C 称为不同的元素。

对于不同类型的指标，有与之对应的不同的贡献率计算方法。

可加型指标波动贡献率的计算

1. 计算逻辑

可加型指标是指那些数值可以直接相加的指标，例如访客数、销量、销售额。这里以一个简单的案例来介绍可加型指标的计算方法，案例数据如表 14- 1 所示。

表 14-1 可加型指标案例数据

总体销售额从活动前的 11800 元上升到活动后的 14300 元，环比增长 $21\mathrm{\%}$ 。总体又可以拆分成 A、B、C 三个渠道，每个渠道活动前后的销售、环比增长率我们已经计算好了。

从环比波动的角度来看，B 和 C 两个渠道波动较大。不过，由于 B、C 两个渠道体量和 A 差了很多，所以它们的波动对于总体波动的影响并不太大，其环比增长率并不能说清楚问题。所以，我们用贡献率来衡量每个渠道对于总体波动的影响。

要计算贡献率，我们先用活动后销售额减活动前销售额，计算出活动前后每个渠道销售额的波动值，如表 14- 2 所示。

表 14-2 可加型指标计算波动值

然后用每个渠道的波动值除以总体波动值，得到每个渠道波动占总体波动的比重，即波动贡献率。A 渠道的波动贡献率 $=\mathrm{A}$ 渠道波动值/总体波动值 $=1000/2500=40\mathrm{\%}$ ，B 渠道的波动贡献率也是 $40\mathrm{\%}$ ，C 渠道的是 $20\mathrm{\%}$ 。具体结果如表 14- 3 所示。

表 14-3 可加型指标波动贡献率计算结果

从波动贡献率可以发现，A 和 B 渠道对于总体波动的贡献（也可以说影响程度）都很大，是主要的影响因素。而 C 渠道虽然环比增长率为 $167\mathrm{\%}$ ，但是受限于体量，其波动贡献率只有 $20\mathrm{\%}$ 。

2. Pandas 实现

构造上面的案例数据，before 和 after 分别指代活动前、活动后销售额：

dl = pd.DataFrame ({'渠道':[ 'A', 'B', 'C'], 'before':[ 11000, 500, 300], 'after':[ 12000, 1500, 800]})

计算环比增长率、波动值和波动贡献率：

dl['环比增长率'] = (dl['after'] - dl['before']) / dl['before'] dl['波动值'] = dl['after'] - dl['before'] dl['波动贡献率'] = dl['波动值'] / dl['波动值']. sum () #用每一行波动值除以总体波动值 #汇总得到贡献率 print (d 1)

运行结果如下：

3. 问题延伸

可加型指标波动贡献率的优缺点都很明显：优点在于简单方便，数据分析师好计算，业务人员好理解，双方容易达成共识；缺点则是对于优先级的判定不够明确。拿上面的案例来说，我们的结论是 A 和 B 渠道是影响总体的两大渠道。如果精力有限，我们应该重点关注 A 渠道还是 B 渠道呢？既可以说 A 渠道体量大，更应该关注和优化，也可以说虽然两个渠道的波动贡献率相等，但是 B 渠道自身的波动远远大于 A 渠道，B 渠道发生异常的可能性更大。

至于应该如何改进，我们将在 14.2 节探讨。接下来，我们继续学习乘法型指标波动贡献率的计算。

乘法型指标波动贡献率的计算

1. 计算逻辑

还记得我们在电商理论部分提到的指标拆解的黄金公式吗？销售额 $\equiv$ 访客数 $x$ 转化率 $x$ 客单价。

如果销售额出现了异常波动，业务人员大概率会循着这个公式来定位问题，判断访客数、转化率、客单价中每个指标的波动情况及影响。

在这个场景下，可加型指标波动贡献率的计算方式是无法解决问题的，因为各指标之间是乘法关系，而且量纲不同，无法直接相加减。想要计算出各指标对于总体指标波动的影响，使用对数转换法是条思路。

下面我们一起来看案例数据，如表 14- 4 所示

表 14-4 乘法型指标案例数据

案例数据中，销售额增长了 $126\mathrm{\%}$ ，访客数和转化率分别提升 $50\mathrm{\%}$ 、 $60\mathrm{\%}$ ，而客单价环比下降 $6\mathrm{\%}$ 要计算这 3 个指标对于销售额的贡献率，可以使用对数转换法（LN 转换）对活动前后访客数、转化率、客单价的每个值进行转换，转换后的值就能够套用可加型指标贡献率的计算方法了。其中 LN 是以常数 e 为底数的对数。计算结果如表 14- 5 所示。

表 14-5 乘法型指标 LN 转换

对活动前的访客数 10000 用 LN（10000）进行转换，得到 9.21；对活动后的访客数与其他指标也都进行这样的转换。经过转换之后，相关值的波动是可以直接计算的，我们计算 LN 波动值（某指标活动后的 LN 转换值- 该指标活动前的 LN 转换值），如表 14- 6 所示。

表 14-6 计算 LN 转换后的波动值

访客数、转化率、客单价的 LN 波动值之和正好等于销售额的 LN 波动值。到这一步，我们可以借用上面介绍的波动占比方法来计算贡献度，用每个元素的 LN 波动值除以总体 LN 波动值（销售额的 LN 波动值），如表 14- 7 所示。

表 14-7 乘法型指标波动贡献率的计算

$\mathrm{①}$ 因为计算过程中存在四舍五入的关系，这里直接计算结果为 $99.99\mathrm{\%}$ ，但实际为 $100\mathrm{\%}$

最终可以得到：首先是转化率的波动贡献率为 $57.55\mathrm{\%}$ ，排名第一；其次是访客数的波动贡献率为 $49.65\mathrm{\%}$ ；而客单价是环比降低的，对应的是负的贡献率。贡献率的总体之和是 $100\mathrm{\%}$ ，逻辑自洽。

2. Pandas 实现

依然先构造数据，这次我们把销售额也直接构造出来：

d 2 = pd.DataFrame ({'指标':[访客数','转化率','客单价','销售额'],
'before':[10000,0.05,350,175000],
'after':[15000,0.08,330,396000]})

计算环比增长率、LN 波动值和波动贡献率：

import numpy as np #numpy的log可以直接转换成对数

d 2['环比增长率'] = (d 2['after'] - d 2['before']) / d 2['before'] d 2['LN_before'] = np.log (d 2['before']) d 2['LN_after'] = np.log (d 2['after']) d 2['LN_波动值'] = d 2['LN_after'] - d 2['LN_before'] d 2['波动贡献率'] = d 2['LN_波动值'] / d 2['LN_波动值'] #总体数据索引是3 ，因此这里用 3 来找到总体值 print (d 2)

运行结果如下：

这样就得到了每个指标对于销售额的波动贡献率。

除法型指标波动贡献率的计算

1. 计算逻辑

像点击率、转化率这样的指标属于除法型指标，对它们的波动贡献率的计算相对复杂，我们以不同渠道的活动前后转化率数据为例，如表 14- 8 所示。（表中，channel 代表渠道，before_cvr 和 after_cvr 分别代表活动前和活动后的支付转化率。）

表 14-8 活动前后转化率的变化

由表 14- 8 可知，整体转化率从活动前的 $27.5\mathrm{\%}$ 下滑至活动后的 $26.2\mathrm{\%}$ ，环比降低 $4.7\mathrm{\%}$ ，其中 A 渠道和 B 渠道的转化率没有变化，C 渠道略微上涨，而 D 渠道降幅明显。我们能据此得出“D 渠道是造成整体转化率下降的唯一元素”的结论吗？

万万不可！因为转化率是一个衍生指标，单看转化率的高低趋势，很容易忽略体量的重要影响。同时，转化率的波动来源于访客数和购买人数两个指标的变化。只有看清楚背后访客数、购买人数的变化情况，才能量化各渠道转化率对总体波动的贡献率。所以，我们需要结合活动前后的访客数 uv 和购买人数 pay 来看，如图 14- 1 所示。

图 14-1 除法型指标相关数据

由访客数和购买人数可以发现，A、B 渠道虽然转化率都未发生变化，但这只是水面的平静。实际上 A 渠道活动后访客数和购买人数均是活动前的 2 倍，而 B 渠道的相关数据完全没有变化。

我们需要把镜头从平静的水面移到水底，看看波澜起于何方。

2. 波动贡献率剖析

要综合访客数、购买人数指标，更好地量化每个渠道转化率对整体转化率的影响，这里我们采用一种类似于控制变量的方法。

首先，我们研究 A 渠道波动对于整体的影响。假设只有 A 渠道的数据活动前后发生了变化，其他渠道均未发生任何变化，即活动后数据与活动前相等，如图 14- 2 所示。

只有 A 渠道发生变化，其他渠道活动前后数据不变：

结果显而易见：

A 渠道访客数环比增长 $100\mathrm{\%}$ ，将整体访客数从 10 万提升到 15 万，环比上涨 $50\mathrm{\%}$

A 渠道的购买人数成倍增长，推动整体购买人数环比提升 $36.4\mathrm{\%}$

访客数和购买人数变化一致，因此 A 渠道转化率不变，但 A 渠道访客数和购买人数对整体产生结构性的影响，造成整体转化率环比降低 $9.1\mathrm{\%}$ ，这 $9.1\mathrm{\%}$ 的降幅可以看作 A 渠道活动前后数据变化对于整体的影响。

根据同样的逻辑，我们对其他渠道进行控制和计算，如图 14- 3 所示。B 渠道活动前后数据均未发生变化，因此对于整体转化率的影响是 $0.0\mathrm{\%}$ ；C 渠道对于整体转化率有 $16.7\mathrm{\%}$ 的正向影响；D 渠道自身转化率就有大幅下滑，对于整体转化率的影响则是 $-13.0\mathrm{\%}$ 。把各渠道的影响汇总一下，得到如表 14- 9 所示的结果。

只有 B 渠道发生变化，其他渠道活动前后数据不变：

图 14-3 其他渠道控制变量的结果

只有 C 渠道发生变化，其他渠道活动前后数据不变：

只有 D 渠道发生变化，其他渠道活动前后数据不变：

表 14-9 各渠道影响的汇总

图 14-3 其他渠道控制变量的结果（续）

通过控制变量，我们得到了每个渠道对于整体转化率的影响。不过，一般提到贡献率的计算，总是希望各渠道贡献率加总接近于 $100\mathrm{\%}$ 。所以，我们用各渠道的影响值除以汇总的影响值，计算对应的贡献率。以 A 渠道为例，用 $-9.1\mathrm{\%}$ 除以各渠道影响值的汇总，等于 $166.3\mathrm{\%}$ ，其他渠道亦是如此，如表 14- 10 所示。

表 14-10 各渠道的贡献率结果

需要注意的是，由于整体转化率是负值，如 A 渠道贡献率为正，则意味着该渠道对整体转化率的负向变化是有贡献的，或者说拉低了整体转化率。反之，如 C 渠道贡献率为负，则代表该渠道对于整体转化率是有拉升作用的。

3. Pandas 实现

下面用 Pandas 完成除法型指标波动贡献率的计算。首先依然是构造数据：

df_uv = pd.DataFrame ({ 'channel':[A,'B','C','D','ALL'], 'before_uv':[50000,10000,30000,10000,100000], 'after_uv':[100000,10000,50000,25000,185000] }) df_pay = pd.DataFrame ({ 'channel':[A,'B','C','D','ALL'], 'before_pay':[10000,1500,15000,1000,27500], 'after_pay':[20000,1500,26000,1000,48500] }) df_cvr = pd.DataFrame ({ 'channel':[A,'B','C','D','ALL'], 'before_cvr':[0.2,0.15,0.5,0.1,0.28], 'after_cvr':[0.2,0.15,0.52,0.04,0.26] })

构造一张活动前后数据均不变的表，为后续的控制变量做准备：

df_uv_con $=$ df_uv.copy () df_uv_con['after_uv'] $=$ df_uv['before_uv'] df_pay_con $=$ df_pay.copy () df_pay_con['after_pay'] $=$ df_pay['before_pay']

df_uv_con 和 df_pay_con 分别对应访客数与购买人数，表的具体内容如下：

接着用控制变量的方式计算 A 渠道的影响，即其他渠道活动前后数据不变，计算 A 渠道数据的变化对整体的影响。

df_uv_con. loc[df_uv_con['channel'] == 'A', :] = df_uv. loc[df_uv['channel'] == 'A', :] df_pay_con. loc[df_pay_con['channel'] == 'A', :] = df_pay. loc[df_pay['channel'] == 'A', :]

把真实的 A 渠道数据用索引的方式进行替换，得到了控制后的表：

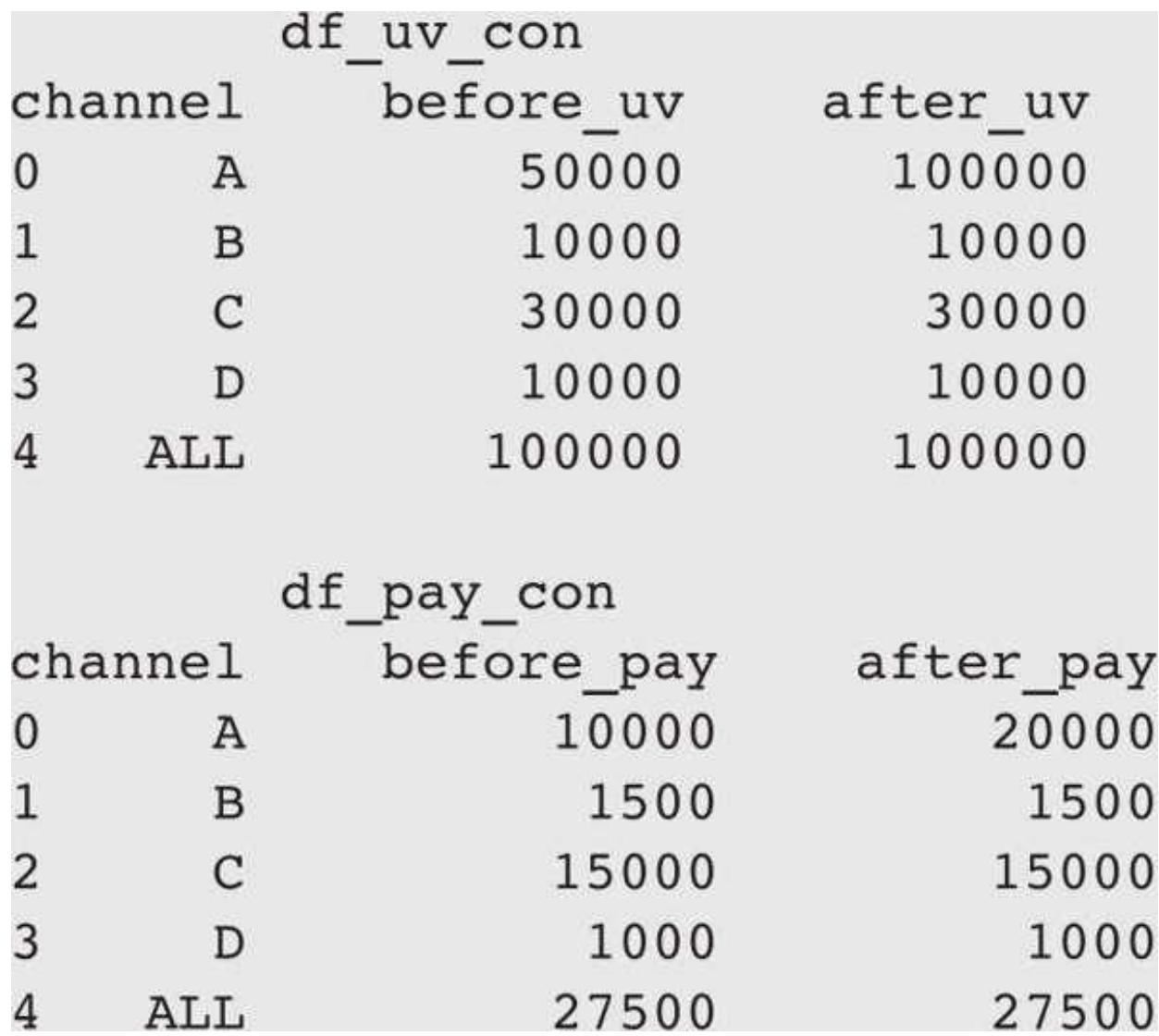
只有 A 渠道发生变化的数据产生了，但是由于用的是索引替换，汇总行的数据并未自动发生变化。在后续计算中我们需要注意重新求汇总。

对活动前后的访客数进行汇总并重新计算

before_uv_sum = df_uv_con['before_uv'][:- 1]. sum () after_uv_sum = df_uv_con['after_uv'][:- 1]. sum ()

对活动前后的购买人数进行汇总并重新计算

before_pay_sum = df_pay_con['before_pay'][:- 1]. sum () after_pay_sum = df_pay_con['after_pay'][:- 1]. sum ()

计算 A 渠道对整体的影响，活动后整体转化率和活动前的环比增长率 before_cvr_all = before_pay_sum / before_uv_sum after_cvr_all = after_pay_sum / after_uv_sum result_a = (after_cvr_all - before_cvr_all) / before_cvr_all

显示 4 位小数的结果，避免小数位太多 print (result_a)

最终得到了结果- 0.0909，和我们在 Excel 中计算的一致。如果要按照同样的逻辑分别计算其他渠道的影响，可以采用循环遍历的方式：

result dic ={}

for channel in df_uv['channel'][:- 1]:

构造控制变量的原始表，活动前后数据相等

df_uv_con $=$ df_uv.copy () df_uv_con['after_uv'] $=$ df_uv['before_uv'] df_pay_con $=$ df_pay.copy () df_pay_con['after_pay'] $=$ df_pay['before_pay']

用索引替换对应渠道的数据 df_uv_con. loc[df_uv_con['channel'] $==$ channel,:] $=$ df_uv. loc[df_uv['channel'] $==$ channel,:] df_pay_con. loc[df_pay_con['channel'] $==$ channel,:] $=$ df_pay. loc[ df_pay['channel'] $==$ channel,:]

对活动前后的访客数进行汇总并重新计算 before_uv_sum $=$ df_uv_con['before_uv'][:- 1]. sum () after_uv_sum $=$ df_uv_con['after_uv'][:- 1]. sum ()

对活动前后的购买人数进行汇总并重新计算 before_pay_sum $=$ df_pay_con['before_pay'][:- 1]. sum () after_pay_sum $=$ df_pay_con['after_pay'][:- 1]. sum ()

计算渠道对整体的影响，活动后整体转化率和活动前的环比率 before_cvr_all $=$ before_pay_sum / before_uv_sum after_cvr_all $=$ after_pay_sum / after_uv_sum result_x $=$ (after_cvr_all- before_cvr_all)/ before_cvr_all

result dic[channel] $=$ result_x

构造最终的影响结果 result $=$ pd.DataFrame (result_dic, index $=$ ['value']). T

print (result)

运行结果如下：

valueA - 0.090909 B 0.000000 C 0.166667 D - 0.130435

计算最终贡献率，只需增加一列求占比即可：

result['贡献率'] = result['value'] / result['value']. sum () print (result)

运行结果如下：

value 贡献率 A - 0.090909 1.662651 B 0.000000 - 0.000000 C 0.166667 - 3.048193 D - 0.130435 2.385542

通过遍历循环，我们计算出了所有渠道对整体转化率波动的贡献率。

14.2 Adtributor 算法

Adtributor 介绍

面对数据波动类问题，我们可以从各种维度来拆解数据。例如，本章开头提到了渠道、新老客、消费力、年龄等维度，每个维度下又有具体的元素，如新老客下有新客和老客，消费力下有低、中、高消费力。

如此多的维度，可谓是“波动拆解深似海，从此分析是路人”。有没有一种方法可以告诉我们最终的指标波动从哪个维度拆解最合适，并明确这个维度下的哪几个元素对整体波动的贡献率最高呢？

Adtributor 算法解决的就是“如何自动归因指标波动”这个问题。该算法由微软研究院提出，通过一套自动化判定的逻辑，拨云见雾，帮助数据分析师快速找到数据异常波动的根本原因。

Adtributor 算法的核心逻辑如图 14- 4 所示

图 14-4 Adtributor 算法的核心逻辑

（图片来源：论文"Adtributor: Revenue Debugging in Aolvertising Systems”，作者为 BHAGWANR、KUMARR 和 RAMJERR 等人）

看不太懂？没关系，我们来一步步拆解。

单个维度的基础案例

下面先介绍一个基础案例，带大家了解算法的基本思路以及每个指标的意义。

1. 计算活动前后基本占比

我们拿到了一份数据，它包含每个渠道的活动前、活动后销售额数据，也有汇总数据，如表 14- 11 所示。

表 14-11 案例数据

先计算活动前和活动后每个渠道的销售额占总体的比重。

设活动前销售额占比为 p，如渠道 A 的 $\mathrm{p}=500000/750000\approx 67\mathrm{\%}$

设活动后销售额占比为 q，如渠道 B 的 $\mathrm{q}=230000/1500000\approx 15\mathrm{\%}$

计算结果如表 14- 12 所示。

表 14-12 计算得到 p 和 q 的值

计算活动前占比 p 和活动后占比 q，是为后续计算惊讶度做准备。

2. 计算惊讶度

通过计算指标波动贡献率，能够较好地衡量每个元素对于总体波动的贡献率，但是却忽略了不同元素自身波动所包含的信息。一个体量小但成倍增长的渠道与一个体量大但波动小的渠道相比，前者或许隐藏着更多的机会。

惊讶度（Surprise，用 S 表示）是一个用来衡量指标结构前后变化程度的指标，回答的是“哪个元素的波动最让人惊讶”的问题。

惊讶度主要考虑前后占比的结构变化，因此上一步的 p 和 q 值是计算的基础。惊讶度的计算一般采用 JS 散度[1]，计算公式如下：

S 值越高，表示该维度的变化惊讶度越高，越有可能是主要的影响因素。

我们把公式用在案例数据上，如表 14- 13 所示

表 14-13 计算得到惊讶度 S 值

可以看到，B 渠道销售额增长 20 万元，而 A 渠道增长 28 万元，A 渠道的销售额增长要高于 B 渠道的销售额增长。但由于 B 渠道的销售额从 3 万元增长到 23 万元，占比从活动前的 4%提升到活动后的 $15\mathrm{\%}$ ，变化最为剧烈，所以 B 的惊讶度 $0.77\mathrm{\%}$ 是所有渠道中最高的，需要重点关注。

3. 计算贡献率 EP

EP 是 ExplanatoryPower 的缩写，在很多地方被翻译成"解释力”，但从衡量的内容及其计算逻辑来看，它就是前几节所讲的贡献率，即每个元素波动对于总体波动的贡献，所以后文中统一将它理解成贡献率。

以 A 渠道为例，A 渠道的 EP $\equiv$ （A 渠道活动后销售额- A 渠道活动前销售额）／（总体活动后销售额- 总体活动前销售额）。

把这个公式应用在案例数据上，计算结果如表 14- 14 所示

表 14-14 计算得到 EP 值

很容易得到每个渠道的变化对于整体波动的贡献率。

4. 结果筛选

要筛选出渠道维度里对整体波动影响最大的两个元素，Adtributor 应该如何操作呢？

口按照惊讶度 S 从高到低对数据进行排序，即数据排序为 B、A、D、C。

口单个元素 EP（波动贡献率）的筛选。如果某个维度存在非常多的元素，为了避免有些元素量级和波动都太小，需要设置一个贡献率的阈值，此处我们设置为 $10\mathrm{\%}$ ，表示单个元素的波动贡献率 EP 超过 $10\mathrm{\%}$ 时才会通过筛选。案例中渠道 D 的 EP 等于 $0\mathrm{\%}$ ，会被剔除，保留 B、A、C 这 3 个符合条件的渠道。

口整体 EP（波动贡献率）的控制。在进行单个波动贡献率筛选的同时，可以设置一个整体贡献率的阈值，如 $60\mathrm{\%}$ ，这意味着只要选中元素贡献率之和超过 $60\mathrm{\%}$ ，就已经能够解释大部分波动原因了，可以停止筛选。

在案例数据中，尽管 C 渠道通过了单个波动贡献率超过 $10\mathrm{\%}$ 的筛选，但由于 B 渠道和 A 渠道的 EP 值相加等于 $64\mathrm{\%}$ ，已经超过整体贡献率的阈值，所以停止遍历。最终，筛选出影响最大的两个元素是 B 和 A。

[1]. 一种用于衡量概率分布相似性的方法，这里用 JS 散度衡量 p 和 q 的变化程度。

多个维度的算法逻辑和 Pandas 实现

上面的案例只考虑了单个渠道，相当于已经选定渠道维度，只需要找出渠道下影响较大的元素。在实际工作中，我们可能会遇到几十、几百甚至上千个维度。面对多维度问题，Adtributor 又是如何解决的呢？

我们用 Pandas 来实现。仍然从案例入手，案例数据包含渠道、新老客、产品三个维度。

data $=$ pd. DataFrame（维度：[渠道，渠道，渠道，渠道，新老客，新老客，产品，产品，产品，产品，产品，产品，产品，]，元素：[A，B，C，D，新客，老客，C 001，C 002，C 003，C 004，C 005，'C 006']，'before:[50,3,18,4,35,40,20,15,10,8,12,10]，'after:[78,23,45,4,60,90,40,38,15,20,17,20]）

为了使案例数据更加具象，我们用 Excel 展示一下，如图 14- 5 所示。

图 14- 5 案例数据的 Excel 展示

1. 计算惊讶度并排序

和单维度处理逻辑类似，我们先根据上一节中的公式计算出每个维度下各元素的 p、q 和 S 的值，并在每个维度下按照 S 降序排列。

p 和 q 的计算非常简单，用 Pandas 实现时考虑一下维度数量即可：

计算活动前销售额汇总和活动后销售额汇总因为有 3 个大维度，直接汇总得到的是 3 倍的销售额，需要除以维度数量，这里 len（data['维度']. unique（)）等于 3 pre_sum $=$ data['before']. sum（）／len（data['维度']. unique（)) aft_sum $=$ data['after']. sum（）／len（data['维度']. unique（)）

计算 p 和 q 值 data['p'] $=$ data['before']/pre_sum data['q'] $=$ data['after']/aft_sum

用 len（）和 unique（）结合统计维度的数量，是为了增强代码的可扩展性，这样无论对于多少个维度，以上代码都是适用的。

惊讶度 S 涉及 math 库的 log 计算，这里我们采用遍历的方式来计算并排序：

import math #创建一个列表用于收集每个s值surprises = [] #遍历计算每一行数据的s值for p, q in zip (data['p'], data['q]): #用JS散度公式 s = 0.5 * (p * math. log 10 (2 * p / (p + q)) + q * math. log 10 (2 * q / (p + q))) surprises.append (s) #把计算好的s列表赋值给datadata ['surprise'] = surprises #每个维度下按照s值排序data . sort_values (['维度','surprise'], ascending=False, inplace=True)data

运行结果如下：

这一步我们得到了所有数据的 S 值，并在每个维度下按照 S 值做了降序排列。

2. 计算贡献率并根据闻值筛选元素

先计算每个维度下所有元素 EP（贡献率）的值，然后根据单个 EP 闻值和总 EP 闻值筛选元素，筛选逻辑和单维度一致。

我们用 Pandas 先计算每一行数据的 EP 值：

计算出总销售波动，3 个维度都在一起，因此也需要除以维度数量 sum_dif $=$ （data['after']. sum（）- data['before']. sum（））／len（data['维度']unique（））

计算每一行数据的 EPdata['EP'] $=$ （data['after']- data['before'])／sum_difdata.head ()

运行结果如下：

进行筛选前，我们先设定单个元素 EP 阈值 teep 和总 EP 阈值 tep，这里将 teep 和 tep 分别设置为 0.2 与 0.8。筛选逻辑和单维度相似：

口根据设定的单个元素 EP 阈值 teep，遍历所有元素的 EP 值是否高于 0.2，如果高于，则通过筛选；口每一次遍历的同时，把每个维度下通过筛选的元素 EP 值累加，如果某维度下累加的 EP 值大于 0.8，则该维度停止筛选。

用 Pandas 实现筛选操作，代码如下：

假设单个 EP 阈值 teep $=0.2$ ，总 EP 阈值 tep $=0.8$ teep $=0.2$ tep $=0.8$ #筛选出EP值大于单个EP阈值teep的元素data_fil $=$ data. loc[data['EP'] $>=$ teep，['维度'，元素'，surprise','EP']新建一个 EP_sum 列，即对每个维度下的 EP 值进行累加，作为与总闻值 tep 对比的辅助列 data_fil['EP_sum'] $=$ data_fil. groupby（'维度'）['EP']，cumsum（）data_fil

剔除掉了 EP 值小于 0.2 的数据，并计算出了每个维度下累加的 EP 值 EP_sum 列，运行结果如下：

由于总体阈值 tep 的限制，我们需要剔除掉 EP_sum 大于总 EP 阈值 tep 的数据。

这里可能有读者会认为，用 Pandas 直接剔除累加 EP 值大于 0.8（总阈值）的数据即可。但需要注意的是，这里总 EP 阈值 tep 被设置为 0.8，假如某维度有 5 个元素，EP 值分别是 0.2、0.2、0.3、0.2、0.1，那么对应的累加 EP 值依次是 0.2、0.4、0.7、0.9、1。

我们会发现当累加的 EP 值等于 0.9 时，满足大于 $80\mathrm{\%}$ 的总阈值条件，因而停止累加。这个时候，返回的数据包含前 4 个元素，对应的 EP_sum 是 0.9，即包含第一个大于总 EP 阈值的元素。也就是说，在根据总 EP 阈值批量筛选时，要剔除的是第二个及之后累加值大于总 EP 阈值的元素。

最后两句话有点口，结合 Pandas 代码会更好理解。

先筛选出大于总阈值的数据

bri = data_fil. loc[data_fil['EP_sum'] >= tep,:]

每个维度下，把超过总阈值的第一个累加 EP 值作为接下来的筛选门槛 bri_dim = bri.groupby ('维度'). head (1) '维度','EP_sum'

把经过单个阈值 teep 筛选后的数据和每个维度筛选门槛相匹配，用于下一步计算，空缺值用总阈值 tep 填充 result = pd.merge (data_fil, bri_dim, left_on = '维度', right_on = '维度', how = 'left'). fillna (teep) result. columns = ['维度', '元素', 'surprise', 'EP', 'EP_sum', 'EP_thres']

剔除大于筛选门槛的数据，即筛选出小于或等于筛选门槛的数据 result = result. loc[result['EP_sum'] <= result['EP_thres'], :]

result

运行结果如下：

案例数据由于没有多个累加值大于总阈值的情况，因此数据变化不大。实际上，经过阈值筛选操作，返回了通过单个维度阈值和总阈值筛选的结果。

3. 返回最终结果

到上一步，我们已经获得了每个维度下通过筛选的元素，接下来在每个维度下汇总各元素的 S 值，得到各维度 S 值的汇总结果。

result_gp = result.groupby ('维度')['surprise']. sum (). reset_index () print (result_gp)

运行结果如下：

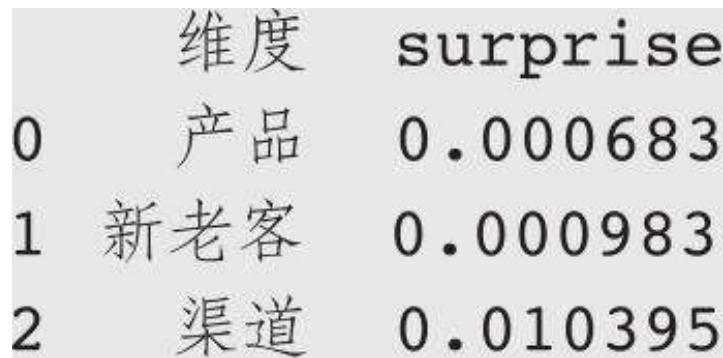
假设我们最终的目标是筛选出影响最大的维度。要实现这个目标，我们只需要按照计算好的各维度 S 汇总值从大到小排序，取排名第一的维度和对应元素的数据：

筛选出影响前 n 的维度 n = 1

每个维度按照 surprise 排序，并返回前 n 个维度

top_n = result_gp. sort_values ('surprise', ascending = False). iloc[: n,:]

根据选择的前 n 个维度，返回维度对应的元素的具体数据 result. loc[result['维度']. isin (top_n['维度']), :]

如此一来，便得到了影响最大的维度和具体的元素，结果如下：

渠道是影响最大的维度，渠道内元素对整体波动的影响从大到小依次是 B、A、C。通过整合上述代码，把阈值设置成参数，用 Pandas 实现的 Adtributor 算法能够帮助我们从成百上千个维度中找到最有可能的根因，并且可以多维度、多元素、交叉探究。

14.3 本章小结

在这一章，我们先学习了贡献率的概念，并用贡献率来衡量每个元素变化对总体波动的影响程度，然后分别熟悉了可加型指标、乘法型指标、除法型指标贡献率的计算方法并用 Pandas 进行实践。

在此基础上，我们还进一步了解了 Adtributor 算法，结合惊讶度、贡献率和对应的阈值筛选，非常高效地定位到影响最大的维度及其元素。

受限于篇幅，Adtributor 的相关内容解决的只是可加型指标的波动定位，比率型指标的计算逻辑也类似，只是贡献率和惊讶度的计算有所差异。相关的 Pandas 代码已经放在本书配套资料中，你只需要设置好筛选用的阈值并确认返回的维度数量，就能定位到对总体波动影响最大的维度及其元素。